Plan sytuacyjny: Różnice pomiędzy wersjami

Wersja z 12:16, 20 paź 2022

W przypadku projektowania łuków z krzywą przejściową (klotoidą) należy wykonać odpowiednie obliczenia, pierwszym etapem jest wyznaczenie parametru A. Aby dobrać parametr A, należy przejść przez kolejne proste obliczenia (warunki).

W tym momencie można przejść do obliczeń parametru A oraz pozostałych parametrów łuku:

Dane wyjściowe z tematu projektu	Dane odczytane z rysunku	Dane odczytane z rozporządzenia
Prędkość do projektowania Klasa techniczna drogi	Kąt zwrotu do 4 miejsc po przecinku	Pochylenie poprzeczne na prostej (domyślnie i₀=2%) Szerokość pasa ruchu Pochylenie poprzeczne na łuku i_p Promień łuku R Przyrost przyspieszenia dośrodkowego k Największe dopuszczalne dodatkowe pochylenie krawędzi jezdni Δi

W pierwszym etapie obliczymy parametr A z kolejnych warunków

Poniższy przykład opiera się na założeniach projektowych:

Klasa techniczna drogi: Z

Prędkość projektowa: 50 km/h

Kąt zwrotu trasy: 30,01232°, co w radianach=0,52381

Warunek 1

A_{min}={\sqrt {Vp \over (3,6^{3}k)}}

W naszym przypadku k=0,8

A_{min}={\sqrt {50 \over (3,6^{3}\cdot 0,8)}}=57,9

Warunek 2

$A_{max}=R{\sqrt {\alpha \,\!}}$

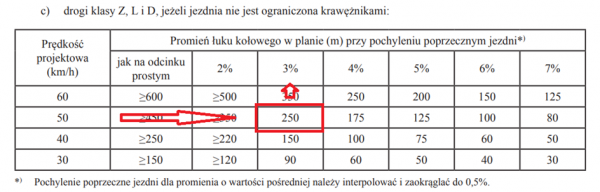
Na podstawie tabeli poniżej przy wstępnie dobranym promieniu łuku o wartości 250 m ustalono, że pochylenie poprzeczne na łuku wynosi ip=3%

$A_{max}=250{\sqrt {0,52381}}=180,9$

Uwaga wartość kąta wstawiamy w Radianach

Warunek 3

$A_{min}={1 \over {3}}R$ oraz $A_{max}=R$

$A_{min}={1 \over {3}}\cdot {250}=86,3$ oraz $A_{max}=250$

Warunek 4

$A_{min}=1,86R^{3 \over {4}}$

$A_{min}=1,86\cdot 250^{3 \over {4}}=116,9$

$A_{max}=2,78R^{3 \over {4}}$

$A_{min}=2,78\cdot 250^{3 \over {4}}=174,8$

Warunek 5

$A_{min}=1,86{\sqrt[{4}]{R^{3}p_{c}}}$

Warunek ten zależy od poszerzenia jezdni na łuku

poszerzenie p wynosi:

p=40/R dla drogi klasy Z i klas wyższych

p=30/R dla drogi klasy L i D

W naszym przypadku

$p={40 \over {250}}=0,16$

ak obliczone poszerzenie należy zaokrąglić do 5 cm zatem w naszym przypadku p=0,20 m. W przypadku jeżeli poszerzenie po zaokrągleniu wynosi mniej niż 0,2 wtedy p=0

Poszerzenie p_c (poszerzenie całkowite) równe jest:

$p_{c}=2p$ w naszym przypadku $p_{c}=2\cdot 0,20=0,40\ m$

zatem:

$A_{min}=1,86{\sqrt[{4}]{250^{3}\cdot 0,4}}=93$

@@ Linia 65: / Linia 65: @@
 Uwaga wartość kąta wstawiamy w Radianach
-=== '''Warunek 2''' ===
+=== '''Warunek 3''' ===
+<math>A_{min}={1\over{3}}R</math>  oraz  <math>A_{max}=R</math>
+<math>A_{min}={1\over{3}}\cdot{250}=86,3</math>    oraz  <math>A_{max}=250</math>
+=== '''Warunek 4''' ===
+<math>A_{min}=1,86R^{3\over{4}}</math>
+<math>A_{min}=1,86\cdot 250^{3\over{4}}=116,9</math>
+<math>A_{max}=2,78R^{3\over{4}}</math>
+<math>A_{min}=2,78\cdot 250^{3\over{4}}=174,8</math>
+=== '''Warunek 5''' ===
+<math>A_{min}=1,86\sqrt[4]{R^3p_c}</math>
+Warunek ten zależy od poszerzenia jezdni na łuku
+poszerzenie p wynosi:
+p=40/R  dla drogi klasy Z i klas wyższych
+p=30/R  dla drogi klasy L i D
+W naszym przypadku
+<math>p={40\over{250}}=0,16</math>
+ak obliczone poszerzenie należy zaokrąglić do 5 cm zatem w naszym przypadku p=0,20 m. W przypadku jeżeli poszerzenie po zaokrągleniu wynosi mniej niż 0,2 wtedy p=0
+Poszerzenie p<sub>c</sub> (poszerzenie całkowite) równe jest:
+<math>p_c=2p</math> w naszym przypadku <math>p_c=2\cdot 0,20=0,40\ m</math>
+zatem:
+<math>A_{min}=1,86\sqrt[4]{250^3\cdot 0,4}=93</math>
+=== '''Warunek 6''' ===

Plan sytuacyjny: Różnice pomiędzy wersjami

Wersja z 12:16, 20 paź 2022